Dijkstra's Algorithm

Dijkstra's Algorithm is a single-source shortest path algorithm proposed by Dutch computer scientist Edsger W. Dijkstra in 1956. It is used to solve the problem of finding the shortest paths from a single source node to all other nodes in a weighted directed or undirected graph (requiring all edge weights in the graph to be non-negative).

I. Core Idea

Greedy Strategy: In each iteration, select the node with the shortest distance to the source node from the set of nodes whose shortest paths have not been determined, and mark it as "determined".Relaxation Operation: Using this node as an intermediary, update the distance from its adjacent nodes to the source node.Repeat the above steps until all nodes are marked as "determined".

II. Algorithm Steps (Taking an Undirected Weighted Graph as an Example)

Assume the graph has n nodes and the source node is s:

Initialization:

• Distance array dist[]: dist[s] = 0 (the distance from the source node to itself is 0), and dist[i] = ∞ (infinity) for all other nodes.
• Mark array visited[]: All nodes are initialized to false (shortest path not determined).
• Priority Queue (Min-Heap): Stores (current distance, node), initialized with (0, s) enqueued. (The naive solution does not use a priority queue.)

Iterative Solution:

1. Extract the node u with the minimum distance from the priority queue; skip if u has been visited.
2. Mark u as visited (visited[u] = true).
3. Traverse all adjacent nodes v of u: if dist[v] > dist[u] + weight(u, v), update dist[v] = dist[u] + weight(u, v) and enqueue (dist[v], v).

Termination Condition:

The priority queue is empty, and the dist[] array now stores the shortest paths from the source node to all nodes. (The naive solution does not use a priority queue.)

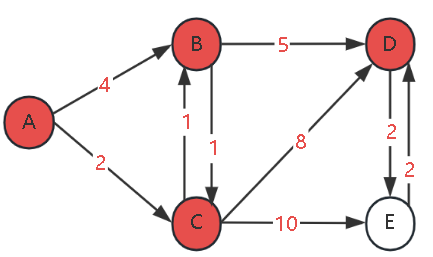
III. Detailed Example

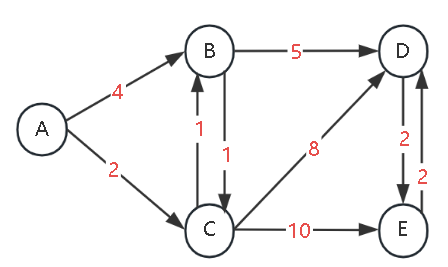
State Table Tracking:

We focus on two states of each node:

• dist[v]: The current known shortest distance estimate from the source node A to node v.
• final[v]: Whether this distance has been confirmed as the final shortest distance (Yes/No).

Algorithm Step-by-Step:

In each step, select the node with the smallest dist value among all nodes where final is "No" for processing.

Step 0: Initialization

Set dist[A] = 0, and ∞ for all other nodes. All nodes are undetermined.

Node	dist	final	Description
A	0	No	Source node
B	∞	No
C	∞	No
D	∞	No
E	∞	No

Current processed node: NoneSelection logic: Prepare to select the node with the smallest dist value from all undetermined nodes.

Step 1: Process Node A

Among all undetermined nodes {A(0), B(∞), C(∞), D(∞), E(∞)}, the smallest dist value is A. Mark it as determined.Check all outgoing edges of A and update the dist values of its neighbors:

• A->B: dist[B] = min(∞, 0+4) = 4
• A->C: dist[C] = min(∞, 0+2) = 2

Updated state:

Node	dist	final	Description
A	0	Yes	Determined
B	4	No	Updated via A
C	2	No	Updated via A
D	∞	No
E	∞	No

Current processed node: ASelection logic: Select the node with the smallest dist value from undetermined nodes {B(4), C(2), D(∞), E(∞)} (i.e., C).

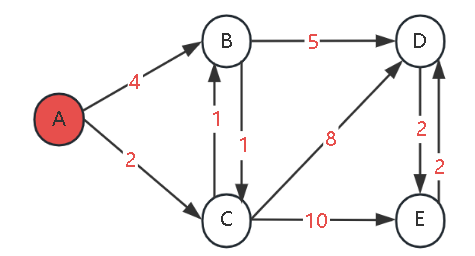
Step 2: Process Node C

Among undetermined nodes, the smallest dist value is C(2). Mark it as determined.Check all outgoing edges of C and update the dist values of undetermined neighbors:

• C->B: dist[B] = min(4, 2+1) = 3 (updated)
• C->D: dist[D] = min(∞, 2+8) = 10
• C->E: dist[E] = min(∞, 2+10) = 12

Updated state:

Node	dist	final	Description
A	0	Yes
B	3	No	Updated via C
C	2	Yes	Determined
D	10	No	Updated via C
E	12	No	Updated via C

Current processed node: CSelection logic: Select the node with the smallest dist value from undetermined nodes {B(3), D(10), E(12)} (i.e., B).

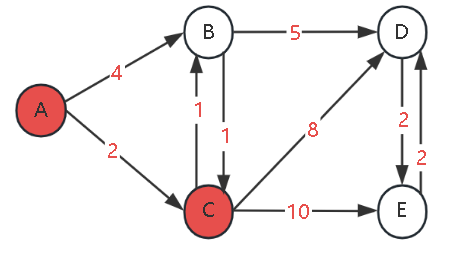
Step 3: Process Node B

Among undetermined nodes, the smallest dist value is B(3). Mark it as determined.Check all outgoing edges of B:

• B->C: C is determined, skip.
• B->D: dist[D] = min(10, 3+5) = 8 (updated)

Updated state:

Node	dist	final	Description
A	0	Yes
B	3	Yes	Determined
C	2	Yes
D	8	No	Updated via B
E	12	No

Current processed node: BSelection logic: Select the node with the smallest dist value from undetermined nodes {D(8), E(12)} (i.e., D).

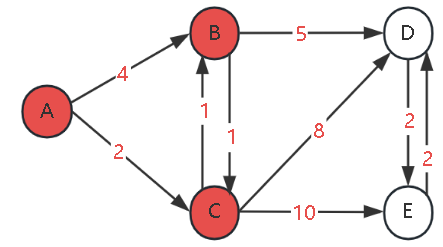
Step 4: Process Node D

Among undetermined nodes, the smallest dist value is D(8). Mark it as determined.Check all outgoing edges of D:

• D->E: dist[E] = min(12, 8+2) = 10 (updated)

Updated state:

Node	dist	final	Description
A	0	Yes
B	3	Yes
C	2	Yes
D	8	Yes	Determined
E	10	No	Updated via D

Current processed node: DSelection logic: Select the node with the smallest dist value from undetermined nodes {E(10)} (i.e., E).

Step 5: Process Node E

The last undetermined node is E(10). Mark it as determined.Check the outgoing edge E->D: D is determined, skip.Final state:

Node	dist	final	Description
A	0	Yes
B	3	Yes
C	2	Yes
D	8	Yes
E	10	Yes	Determined

Current processed node: ESelection logic: All nodes are determined; the algorithm terminates.

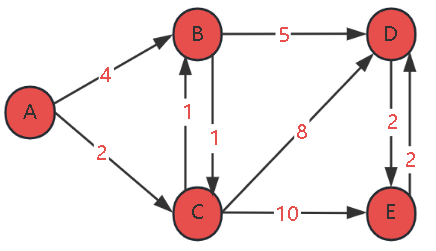
Final Results

Shortest distances from source node A to all nodes:

• A: 0
• C: 2
• B: 3
• D: 8
• E: 10

Process Summary:

1. Initialize the distance (dist) and confirmation state (final) of all nodes.
2. Repeat the following steps until final is "Yes" for all nodes:a. Select: Choose the node u with the smallest dist value among all nodes where final is "No".b. Confirm: Mark final[u] as "Yes". At this point, dist[u] is the final shortest distance from A to u.c. Relax: For each neighbor v of u (and v is undetermined), attempt to update dist[v] with dist[u] + weight(u, v) if it is smaller.
3. The final values in the dist column of the table are the shortest path distances.

IV. Reference Code

1. Naive Solution

#include <iostream>
#include <climits>

using namespace std;

const int MAX_N = 100;  // Maximum number of nodes
int graph[MAX_N][MAX_N];  // Adjacency matrix
int dist1[MAX_N];  // Distance array for Method 1
int dist2[MAX_N];  // Distance array for Method 2
bool visited[MAX_N];  // Visit mark array
int n;  // Actual number of nodes

// Naive Dijkstra's algorithm implementation (without STL)
void dijkstra_naive_no_stl(int src) {
    // Initialization
    for (int i = 0; i < n; i++) {
        dist1[i] = INT_MAX;  // Initialize distance to infinity
        visited[i] = false; // All nodes are unvisited
    }
    
    // Set distance of source node to 0
    dist1[src] = 0;
    
    // Need to process n nodes
    for (int i = 0; i < n; i++) {
        // Step 1: Find the node with the minimum distance among undetermined nodes
        int u = -1;
        int min_dist = INT_MAX;
        
        for (int j = 0; j < n; j++) {
            if (!visited[j] && dist1[j] < min_dist) {
                min_dist = dist1[j];
                u = j;
            }
        }
        
        // If no processable node is found (graph is disconnected), terminate early
        if (u == -1) break;
        
        // Step 2: Mark the node as determined
        visited[u] = true;
        
        // Step 3: Relaxation operation - update distances of all neighbors
        for (int v = 0; v < n; v++) {
            // If there is an edge from u to v (graph[u][v] != 0)
            if (graph[u][v] != 0 && !visited[v] && dist1[u] != INT_MAX) {
                int new_dist = dist1[u] + graph[u][v];
                if (new_dist < dist1[v]) {
                    dist1[v] = new_dist;
                }
            }
        }
    }
}

// Version using adjacency matrix (more naive)
void dijkstra_adj_matrix(int src) {
    // Initialize visited array
    for (int i = 0; i < n; i++) {
        visited[i] = false;
    }
    
    // Initialize distance array
    for (int i = 0; i < n; i++) {
        dist2[i] = graph[src][i] == 0 ? INT_MAX : graph[src][i];
    }
    
    dist2[src] = 0;
    visited[src] = true;
    
    // Process the remaining n-1 nodes
    for (int count = 0; count < n - 1; count++) {
        // Find the unvisited node with the minimum distance
        int u = -1;
        int min_dist = INT_MAX;
        
        for (int i = 0; i < n; i++) {
            if (!visited[i] && dist2[i] < min_dist) {
                min_dist = dist2[i];
                u = i;
            }
        }
        
        if (u == -1) break;
        visited[u] = true;
        
        // Update distances to other nodes via u
        for (int v = 0; v < n; v++) {
            if (!visited[v] && graph[u][v] != 0 && dist2[u] != INT_MAX) {
                int new_dist = dist2[u] + graph[u][v];
                if (new_dist < dist2[v]) {
                    dist2[v] = new_dist;
                }
            }
        }
    }
}

// Initialize the graph
void init_graph() {
    // Initialize adjacency matrix to 0 (indicating no edge)
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            graph[i][j] = 0;
        }
    }
    
    // Example: Build the same graph as before
    n = 5;  // Number of nodes: A(0), B(1), C(2), D(3), E(4)
    
    // Add edges (represented by adjacency matrix)
    // Note: 0 means no edge, other values represent edge weights
    graph[0][1] = 4;  // A->B (4)
    graph[0][2] = 2;  // A->C (2)
    
    graph[1][2] = 1;  // B->C (1)
    graph[1][3] = 5;  // B->D (5)
    
    graph[2][1] = 1;  // C->B (1)
    graph[2][3] = 8;  // C->D (8)
    graph[2][4] = 10; // C->E (10)
    
    graph[3][4] = 2;  // D->E (2)
    
    graph[4][3] = 2;  // E->D (2)
}

int main() {
    // Initialize the graph
    init_graph();
    
    // Calculate shortest paths starting from node 0 (A)
    int src = 0;
    
    cout << "Method 1: Naive implementation with adjacency list logic" << endl;
    dijkstra_naive_no_stl(src);
    
    cout << "Method 2: Naive implementation with adjacency matrix" << endl;
    dijkstra_adj_matrix(src);
    
    // Output results
    char node_names[] = {'A', 'B', 'C', 'D', 'E'};
    
    cout << "\nShortest distances from node " << src << " (A) to all nodes:" << endl;
    cout << "Node\tMethod 1\tMethod 2" << endl;
    cout << "----------------------" << endl;
    
    for (int i = 0; i < n; i++) {
        cout << node_names[i] << "\t";
        
        if (dist1[i] == INT_MAX) {
            cout << "INF";
        } else {
            cout << dist1[i];
        }
        
        cout << "\t";
        
        if (dist2[i] == INT_MAX) {
            cout << "INF";
        } else {
            cout << dist2[i];
        }
        
        cout << endl;
    }
    
    return 0;
}

2. Priority Queue Solution

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
typedef pair<int, int> pii;  // Custom type alias 

/**
 * Dijkstra's Algorithm - Adjacency List + Priority Queue Version
 *  n: Number of nodes (0 ~ n-1)
 *  adj: Adjacency list, adj[u] = vector<{v, w}> meaning edge u->v with weight w
 *  src: Source node
 * Return: Shortest distances from the source node to all nodes
 */
vector<int> dijkstra(int n, vector<vector<pii>>& adj, int src) {
    vector<int> dist(n, INT_MAX); // Initialize distance array 
    vector<bool> visited(n, false); // Initialize mark array 
    priority_queue<pii, vector<pii>, greater<pii>> pq;  // Min-heap (sorted by first element in ascending order by default) 
    dist[src] = 0;
    pq.push(make_pair(0, src)); // make_pair deduces type automatically 
    while (!pq.empty()) {
        pii current = pq.top(); // Head of the priority queue 
        pq.pop();
        int d = current.first; // Current shortest distance from source to node u
        int u = current.second; // Node 
        // Skip if this distance is outdated
        if (d > dist[u]) continue;
        // Mark as visited
        visited[u] = true;
        // Traverse all neighbors
        for (int i = 0; i < adj[u].size(); i++) {
            int v = adj[u][i].first; // Get neighbor node number
            int w = adj[u][i].second; // Get weight of edge u->v
            if (!visited[v]) {
                int new_dist = dist[u] + w;
                if (new_dist < dist[v]) {
                    dist[v] = new_dist;  // Update distance to v 
                    pq.push(make_pair(new_dist, v));// Store distance first, then node in pq 
                }
            }
        }
    }
    return dist;
}

int main() {
    int n = 5;  // Number of nodes
    vector<vector<pii>> adj(n);
    // Build the graph
    adj[0].push_back(make_pair(1, 4));
    adj[0].push_back(make_pair(2, 2));
    adj[1].push_back(make_pair(2, 1));
    adj[1].push_back(make_pair(3, 5));
    adj[2].push_back(make_pair(1, 1));
    adj[2].push_back(make_pair(3, 8));
    adj[2].push_back(make_pair(4, 10));
    adj[3].push_back(make_pair(4, 2));
    adj[4].push_back(make_pair(3, 2));
    
    int src = 0;
    vector<int> dist = dijkstra(n, adj, src);

    cout << "Shortest distances from node " << src << " to all nodes:" << endl;
    for (int i = 0; i < n; i++) {
        if (dist[i] == INT_MAX)
            cout << i << ": INF" << endl;
        else
            cout << i << ": " << dist[i] << endl;
    }
    return 0;
}

Notes:

typedef pair<int, int> pii;  // Custom type alias 

This defines a custom type alias. A common usage in programming is:

typedef long long ll; 

In addition, the meanings of first and second differ in two places: for pii, it only represents a pair of two int values, and the specific meaning is determined by the user.

3. Dijkstra's Algorithm with Path Recording

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <algorithm> // Used for reverse to invert the path
using namespace std;
typedef pair<int, int> pii;  // Custom type alias 

/**
 * Dijkstra's Algorithm - Adjacency List + Priority Queue Version (with Path Recording)
 *  n: Number of nodes (0 ~ n-1)
 *  adj: Adjacency list, adj[u] = vector<{v, w}> meaning edge u->v with weight w
 *  src: Source node
 *  path: Output parameter: path[v] stores the predecessor node of v (used to backtrack the path)
 * Return: Shortest distances from the source node to all nodes
 */
vector<int> dijkstra(int n, vector<vector<pii>>& adj, int src, vector<int>& path) {
    vector<int> dist(n, INT_MAX); // Distance array: shortest distance from src to each node
    vector<bool> visited(n, false); // Mark array: whether the node's shortest distance is determined
    priority_queue<pii, vector<pii>, greater<pii>> pq;  // Min-heap (sorted by distance in ascending order)

    // Initialization: path array initialized to -1 (indicating no predecessor node)
    path.assign(n, -1);
    dist[src] = 0;
    pq.push(make_pair(0, src)); 

    while (!pq.empty()) {
        pii current = pq.top(); 
        pq.pop();
        int d = current.first; // Current distance from src to u
        int u = current.second; // Current node

        // Skip if distance is outdated (a shorter path has been found)
        if (d > dist[u]) continue;
        visited[u] = true;

        // Traverse all neighbors of u
        for (int i = 0; i < adj[u].size(); i++) {
            int v = adj[u][i].first; // Neighbor node
            int w = adj[u][i].second; // Edge weight
            if (!visited[v]) {
                int new_dist = dist[u] + w;
                // Find a shorter path: update distance + record predecessor node
                if (new_dist < dist[v]) {
                    dist[v] = new_dist;
                    path[v] = u; // Record u as the predecessor of v
                    pq.push(make_pair(new_dist, v));
                }
            }
        }
    }
    return dist;
}

/**
 * Backtrack the path: reverse from target node to source node, then invert to get the forward path
 *  src: Source node
 *  target: Target node
 *  path: Predecessor node array
 * Return: Shortest path from src to target (forward order)
 */
vector<int> getShortestPath(int src, int target, const vector<int>& path) {
    vector<int> res;
    // Return empty path if target node is unreachable
    if (path[target] == -1 && src != target) {
        return res;
    }
    // Backtrack from target to src
    for (int cur = target; cur != -1; cur = path[cur]) {
        res.push_back(cur);
    }
    // Invert to get forward path (src -> ... -> target)
    reverse(res.begin(), res.end());
    return res;
}

int main() {
    int n = 5;  // Number of nodes (0~4)
    vector<vector<pii>> adj(n);
    // Build the graph
    adj[0].push_back(make_pair(1, 4));
    adj[0].push_back(make_pair(2, 2));
    adj[1].push_back(make_pair(2, 1));
    adj[1].push_back(make_pair(3, 5));
    adj[2].push_back(make_pair(1, 1));
    adj[2].push_back(make_pair(3, 8));
    adj[2].push_back(make_pair(4, 10));
    adj[3].push_back(make_pair(4, 2));
    adj[4].push_back(make_pair(3, 2));
    
    int src = 0;
    vector<int> path; // Store predecessor nodes of each node
    vector<int> dist = dijkstra(n, adj, src, path);

    // Output shortest distances + shortest paths
    cout << "Shortest distances and paths from node " << src << " to all nodes:" << endl;
    for (int i = 0; i < n; i++) {
        cout << "Node " << i << ": ";
        if (dist[i] == INT_MAX) {
            cout << "INF (No path)" << endl;
        } else {
            cout << "Distance=" << dist[i] << ", Path: ";
            vector<int> shortest_path = getShortestPath(src, i, path);
            // Output path
            for (int j = 0; j < shortest_path.size(); j++) {
                if (j > 0) cout << " -> ";
                cout << shortest_path[j];
            }
            cout << endl;
        }
    }
    return 0;
}

/*
Shortest distances and paths from node 0 to all nodes:
Node 0: Distance=0, Path: 0
Node 1: Distance=3, Path: 0 -> 2 -> 1
Node 2: Distance=2, Path: 0 -> 2
Node 3: Distance=8, Path: 0 -> 2 -> 1 -> 3
Node 4: Distance=10, Path: 0 -> 2 -> 1 -> 3 -> 4
*/

Key Explanations:

1. path array:
   • Type: vector<int>, path[v] = u means "In the shortest path to node v, the previous node of v is u".
   • Initialization: All elements are set to -1 (indicating no predecessor node; the source node's predecessor is always -1).
   • Update logic: When a shorter path to node v is found, update path[v] = u synchronously (u is the current node).
2. getShortestPath function:
   • Function: Backtrack from the target node to the source node via the path array.
   • Processing: The backtracked path is in reverse order (target -> ... -> src), so reverse is used to invert it to the forward path.
   • Boundary: If path[target] == -1 and target != src, the target node is unreachable, return an empty path.